Schalttag 2024: Darum gibt es heute den 29. Februar – hüpfendes Google-Doodle zelebriert das Schaltjahr

 

Es ist der 29. Februar, wir befinden uns in einem Schaltjahr, und der Februar ist somit wieder einen Tag länger als gewohnt – verlängert um den Schalttag. Damit niemand die Besonderheit dieses Tages übersieht, feiert Google auch heute wieder das Schaltjahr mit einem interessanten animierten Google-Doodle auf allen internationalen Startseiten. Das heutige Doodle ist von den letzten Schaltjahr-Doodles inspiriert und zeigt einen hereinhüpfenden Tag in Tierform.

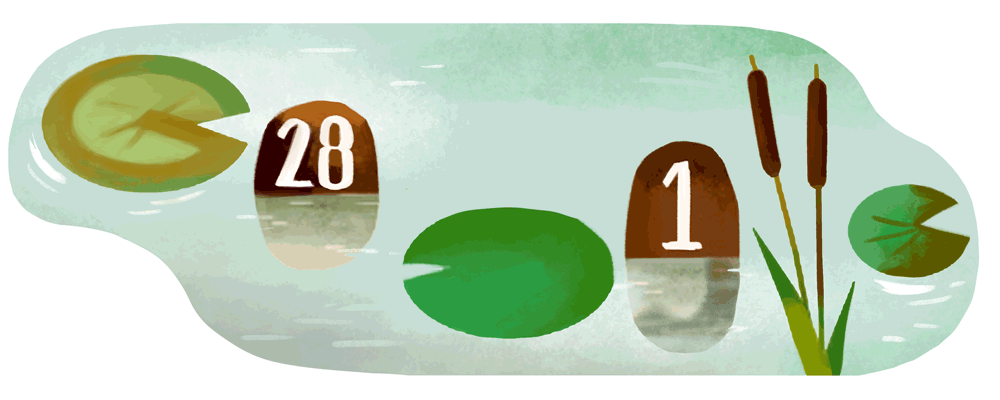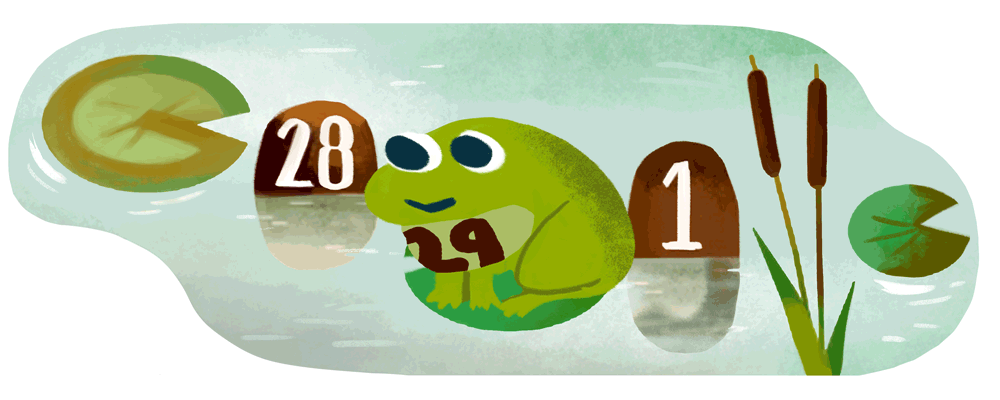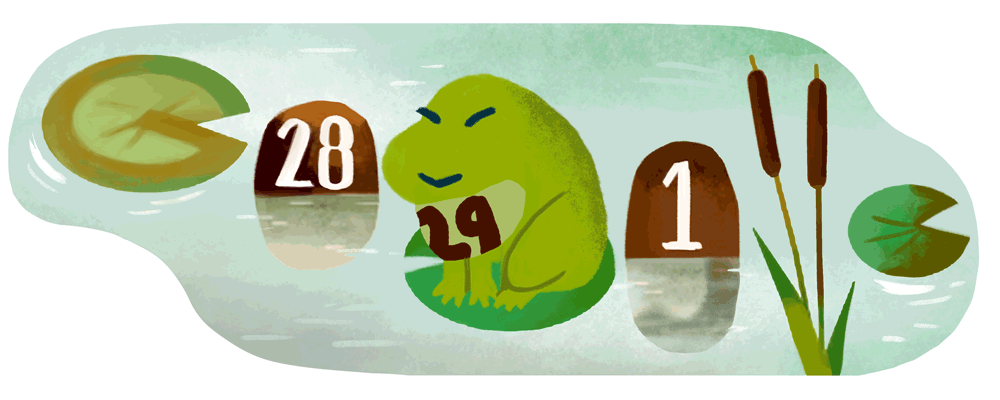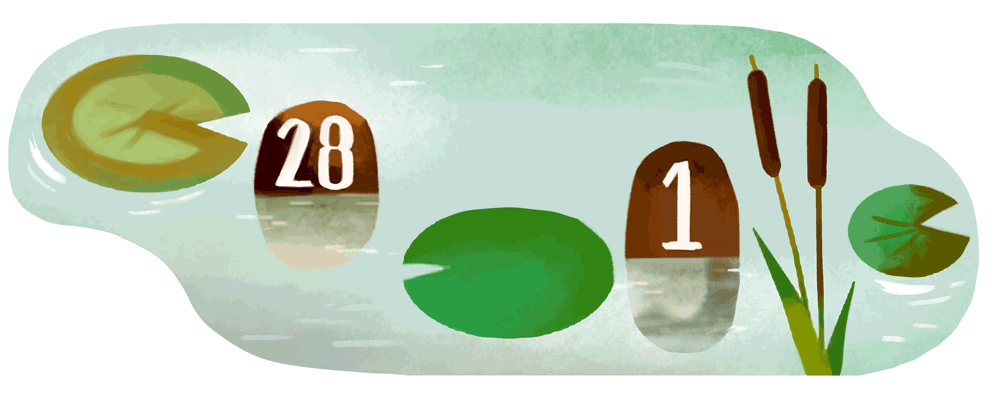
Das heutige Google-Doodle zum Schaltjahr bzw. Schalttag ist auch in diesem Jahr wieder animiert – sowie schon in den Jahren zuvor. Vor vier Jahren ließ man Buchstaben und Zahlen springen, vor acht Jahren ein Kaninchen und diesmal darf der Frosch ran. Allerdings springt der diesmal nicht zwischen zwei Artgenossen, sondern in einen Tümpel mit Seerosen sowie Steinen.

Die Szenerie zeigt zuerst den Tümpel mit den zwei deutlich sichtbaren Steinen des 28. Februar und 1. März – ein normaler Monatswechsel. Doch dann kommt der Frosch mit einer aufgemalten 29 angesprungen und schiebt sich zwischen diese beiden Tage. Aus dem Leap Day wird ein Frog Day. Und damit wir die Zahl auf dem Bauch des Frosches nicht übersehen, wird diese mit einem lauten Quaack noch einmal sehr groß dargestellt.

Der Google-Schriftzug wird heute durch die Elemente geformt, die in diesem Tümepel schwimmen. Zuerst die Seerosa, dann ein herausstehender Stein, dann wieder eine Seerose, gefolgt von einem weiteren Stein und auch das letzte ‚e‘ ist wieder eine Seerose. Wie üblich hat das ‚l‘ auch diesmal wieder einen Spezialauftritt und wird durch wachsendes Schilf dargestellt.

Letzte Aktualisierung am 21.04.2024 / Bilder von der Amazon Product Advertising API / Affiliate Links, vielen Dank für eure Unterstützung!

Warum gibt es den 29. Februar 2020?
Ihr werdet es mitbekommen haben, den 29. Februar gibt es nur alle vier Jahre im sogenannten Schaltjahr und in diesem Jahr ist es wieder soweit. Alle vier Jahre wird ein Schaltjahr eingeschoben, um unseren gregorianischen Kalender wieder mit dem Sonnenkalender anzugleichen. Eigentlich müssten unsere Jahre nicht 365 Tage, sondern 365,24219 Tage haben. Weil das aber sehr unpraktisch ist, schiebt man einfach alle vier Jahre einen Tag ein und schon passt es ungefähr wieder. Die kleine Differenz wird mit anderen Mitteln ausgeglichen. Als man den „Fehler“ vor 440 Jahren bemerkte, hatte Papst Gregor XIII einfach angeordnet, zehn Tage aus dem Kalender verschwinden zu lassen. Lest dazu auch den folgenden interessanten Abschnitt aus Wikipedia.

1582 fand die Frühlingstagundnachtgleiche nach dem julianischen Kalender schon am 11. März statt. Für den Tag des Frühlingsanfangs war aber der 21. März festgelegt (erste Konzil von Nicäa im Jahr 325). Die aufgelaufene Differenz betrug somit 10 Tage. Auf Anordnung von Papst Gregor XIII. wurden 1582 zehn Kalendertage ausgelassen (auf den 4. Oktober folgte der 15. Oktober, wobei die Abfolge der Wochentage nicht verändert wurde: auf einen Donnerstag folgte ein Freitag). Damit künftig kein (oder kein wesentliches) Auseinanderlaufen zwischen Sonnen- und Kalenderjahr stattfindet, wurde die julianische vierjährige Schalttagsregelung ergänzt. Die gregorianische Schalttagsregelung besteht aus folgenden drei einzelnen Regeln:

• Die durch 4 ganzzahlig teilbaren Jahre sind, abgesehen von den folgenden Ausnahmen, Schaltjahre.
• Säkularjahre, also die Jahre, die ein Jahrhundert abschließen (z. B. 1800, 1900, 2100 und 2200) sind, abgesehen von der folgenden Ausnahme, keine Schaltjahre.
• Die durch 400 ganzzahlig teilbaren Säkularjahre, zum Beispiel das Jahr 2000, sind jedoch Schaltjahre.

In 400 Jahren gibt es also 97 Schaltjahre (und ebenso viele Schalttage). Die mittlere Länge eines gregorianischen Kalenderjahres beträgt damit 365 97⁄400 Tage (als Dezimalbruch: 365,2425 Tage).

Seit dieser Regelung beträgt der Fehler bei der Länge des durchschnittlichen Kalenderjahres einen Tag pro ungefähr 3231 Jahren, da das tropische Jahr (365 Tage, 5 Stunden, 48 Minuten, 45,216 Sekunden) dem gregorianischen Kalenderjahr (365 Tage, 5 Stunden, 49 Minuten, 12 Sekunden) um 26,739 Sekunden hinterherläuft. So muss voraussichtlich um das Jahr 4813 (Jahr 1582 + 3231 Jahre) ein Schalttag ausfallen, um das Kalenderdatum 21. März wieder in der Nähe des Zeitpunkts des Primar-Äquinoktiums zu positionieren.

» GMail: Google zieht tatsächlich schon bald den Stecker – aber nur einer älteren Funktion (HTML-Ansicht)

» Android: Microsoft Copilot ersetzt Google Assistant, Gemini und Co – kann als Standard eingestellt werden

» Gemini: KI-Bildgenerator ist ‚absolut inakzeptabel‘ und völlig falsch – Statement von Google-CEO Sundar Pichai

[Wikipedia]

Letzte Aktualisierung am 17.04.2024 / Bilder von der Amazon Product Advertising API / Affiliate Links, vielen Dank für eure Unterstützung!

---

---